Binary search is an efficient algorithm for finding an item from an ordered list of items. It works by repeatedly dividing in half the portion of the list, until narrowing down the possible locations to just one. The time complexity reduces from O(n) to O(logn).
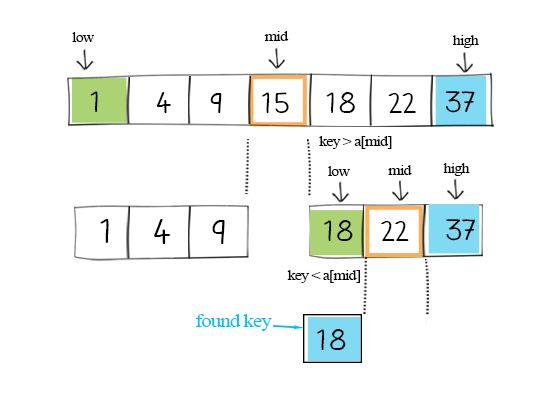
Table of Content
How does binary search work?
Binary search repeatedly compares the key with the item in the middle of a sorted array, until narrows down to just one.
What is the time complexity of binary search?
Binary search skips half of the comparisons after each iteration. The search time reduces from O(n) to O(logn). Binary search is fast.
Iterative solution
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Solution 1, Iteration, Time O(logn), Space O(1), n is array length public static int binarySearch(int[] arr, int key) { int low = 0; int high = arr.length - 1; while (low <= high) { int mid = low + (high-low)/2; if (arr[mid] == key) return mid; else if (key < arr[mid]) high = mid - 1; else low = mid + 1; } return -1; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Solution 1, Iteration, Time O(logn), Space O(1) function binarySearch(arr, key) { var low = 0; var high = arr.length - 1; while (low <= high) { let mid = parseInt(low + (high-low)/2); if (arr[mid] == key) return mid; else if (key < arr[mid]) high = mid - 1; else low = mid + 1; } return -1; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 | #Solution 1, Iteration, Time O(logn), Space O(1) def binarySearch(arr, key) : low = 0 high = len(arr) - 1 while low <= high : mid = low + (high-low)//2 if arr[mid] == key : return mid elif key < arr[mid] : high = mid - 1 else : low = mid + 1 return -1 |
Doodle

Recursive solution
Java
1 2 3 4 5 6 7 8 9 10 11 12 | //Solution 2, Recursion, Time O(logn), Space O(logn) public static int binarySearchRec(int[] arr, int key, int low, int high) { if (low > high) return -1; int mid = low + (high-low)/2; if (arr[mid] == key) return mid; else if (key < arr[mid] ) return binarySearchRec(arr, key, low, mid-1); else return binarySearchRec(arr, key, mid+1, high); } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 | //Solution 2, Recursion, Time O(logn), Space O(logn) function binarySearchRec(arr, key, low, high) { if (low > high) return -1; let mid = parseInt(low + (high-low)/2); if (arr[mid] == key) return mid; else if (key < arr[mid] ) return binarySearchRec(arr, key, low, mid-1); else return binarySearchRec(arr, key, mid+1, high); } |
Python
1 2 3 4 5 6 7 8 9 10 11 | #Solution 2, Recursion, Time O(logn), Space O(logn) def binarySearchRec(arr, key, low, high) : if low > high : return -1 mid = low + (high-low)//2 if (arr[mid] == key) : return mid elif key < arr[mid] : return binarySearchRec(arr, key, low, mid-1) else : return binarySearchRec(arr, key, mid+1, high) |
Free download
Download Java, JavaScript and Python code
Algorithm types and algorithm examples