Catalan number follows the formula of (2n)!/(n+1)!n!. The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, … In this post, we are going to find the n-th Catalan number for any given n. There are 3 solutions. They are iteration, recursion, and dynamic programming.
Table of content
Iterative solution
This solution applies the following alternative expression of Cn. It can be implemented with iteration. It has the best time complexity O(n).
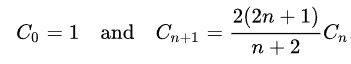
Java
|
1 2 3 4 5 6 7 8 9 |
//Iteration, using formula C0=1 Cn+1= 2(2n+1)/(n+2)*Cn //Time O(Cn) Space O(1), n is input number public static long catalanIte(int n) { long res = 1; for (int i = 0; i < n; i++) { res = res * 2*(2*i+1) / (i+2); } return res; } |
Javascript
|
1 2 3 4 5 6 7 8 9 |
//Iteration, using formula C0=1 Cn+1= 2(2n+1)/(n+2)*Cn //Time O(Cn) Space O(1), n is input number function catalanIte(n) { var res = 1; for (let i = 0; i < n; i++) { res = res *2*(2*i+1) / (i+2); } return res; } |
Python
|
1 2 3 4 5 6 7 |
# Iteration, using formula C0=1 Cn+1= 2(2n+1)/(n+2)*Cn # Time O(Cn) Space O(1), n is input number def catalanIte(n) : res = 1 for i in range(0, n) : res = res *2*(2*i+1) / (i+2) return int(res) |
Recursive solution
This solution uses another alternative expression of Cn. It can be implemented with recursion. It has the worst time complexity O(2^n) with repeated calls.
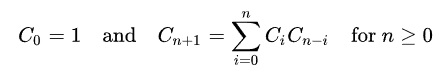
Java
|
1 2 3 4 5 6 7 8 9 10 11 |
//Recursion, formula C0=1, Cn = C0*Cn-1+C1*Cn-2..+ Cn-i*C0 //Time O(2^n), Space O(2^n) public static long catalanRec(int n) { if (n <= 1) // Base condition return 1; int res = 0; for (int i = 0; i < n; i++) { res += catalanRec(i) * catalanRec(n-i-1); } return res; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 |
//Recursion, formula C0=1, Cn = C0*Cn-1+C1*Cn-2..+ Cn-i*C0 //Time O(2^n), Space O(2^n) function catalanRec(n) { if (n <= 1) // Base condition return 1; var res = 0; for (let i = 0; i < n; i++) { res += catalanRec(i) * catalanRec(n-i-1); } return res; } |
Python
|
1 2 3 4 5 6 7 8 9 |
# Recursion, formula C0=1, Cn = C0*Cn-1+C1*Cn-2..+ Cn-i*C0 # Time O(2^n), Space O(2^n) def catalanRec(n): if n <= 1: return 1 res = 0 for i in range(n): res += catalanRec(i) * catalanRec(n-i-1) return res |
Doodle
Dynamic programming
This solution uses the same expression as recursion. But it overcomes the overlapping in recursion by using dynamic programming technique tabulation. The result from previous calls are saved to a 2d array. They can be re-used for the following steps without calling the recursion. It improves the time complexity from exponential to O(n^2).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Dynamic programming, Time O(n^2), Space O(n) public static long catalanDP(int n) { if (n <= 1) return 1; int dp[] = new int[n+1]; dp[0] = 1; dp[1] = 1; for (int i = 2; i <= n; i++) { dp[i] = 0; for (int j = 0; j < i; j++) { dp[i] += dp[j] * dp[i-j-1]; } } return dp[n]; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
//Dynamic programming, Time O(n^2), Space O(n) function catalanDP(n) { var dp = []; dp[0] = 1; dp[1] = 1; for (let i = 2; i <= n; i++) { dp[i] = 0; for (let j = 0; j < i; j++) { dp[i] += dp[j] * dp[i-j-1]; } } return dp[n]; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#Dynamic programming, Time O(n^2), Space O(n) def catalanDP(n) : if n <= 1: return 1 dp = [0]*(n+1) dp[0] = 1 dp[1] = 1 for i in range(2, n+1) : dp[i] = 0 for j in range(0, i): dp[i] += dp[j] * dp[i-j-1] return dp[n] |
Download
Download Catalan number in Java, JavaScript and Python
View animation of finding nth Catalan number in recursion
Numbers and recursions doodle compilation(YouTube)
What are Catalan numbers?
Catalan number follows the formula of (2n)!/(n+1)!n!. The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
What are Catalan numbers used for?
Catalan numbers occur in many counting problems in combinatorics, such as counting the number of ways to generate n pairs of valid parentheses, and counting the number of full binary trees with n+1 leaves.