A graph is a data structure that consists of a set of nodes connected by edges. Graphs are used to simulate many real-world problems, such as routes in cities, circuit networks, and social networks. This is an adjacency list graph implementation 1 – an unweighted graph.
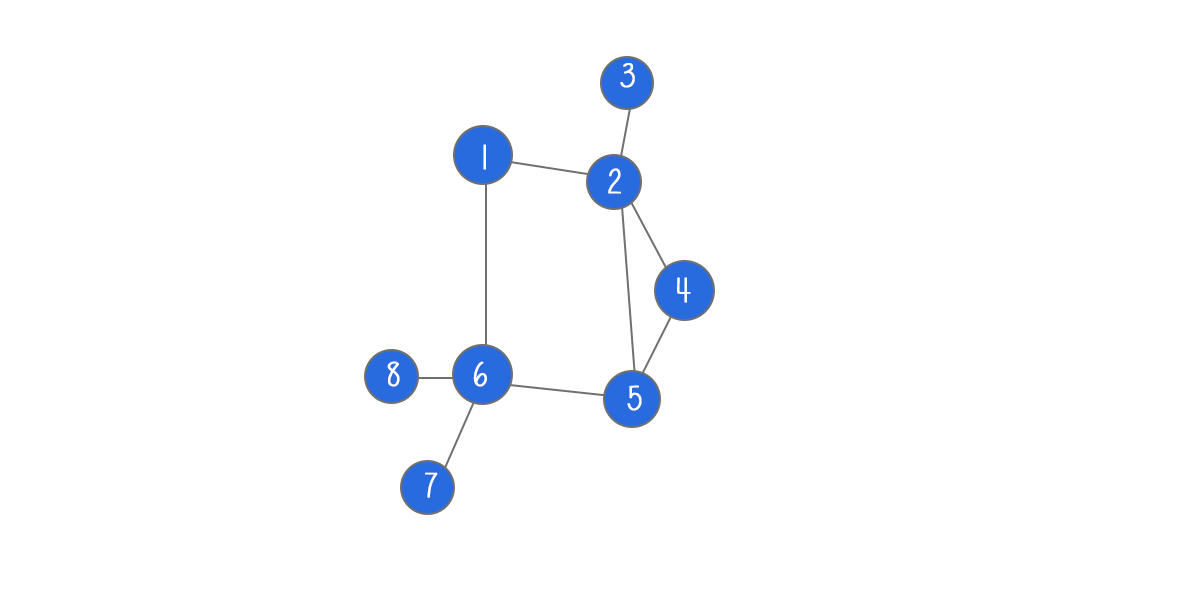
Table of Content
- Terminology
- Map of graph implementations
- Add node and edge
- Remove node and edge
- Search by node and edge
- Find path with DFS in graph
- Find path with BFS in graph
- print graph as adjacency list
- Traverse with DFS in graph
- Traverse with BFS in graph
- Free download
Terminology
A node in the graph is also called a vertex. A line between two nodes is an edge. Two nodes are adjacent, called neighbors if they are connected through an edge. A path represents a sequence of edges between the two nodes.
In a directed graph, all of the edges represent a one-way relationship. In an undirected graph, all edges are bidirectional.
If the edges in the graph have weights (represent costs or distances), the graph is said to be a weighted graph. If the edges do not have weights, the graph is said to be unweighted.
A graph can be presented as an adjacency list or adjacency matrix.
What is an adjacency list?
An adjacency list is a “list of lists”, i.e. a list of nodes, with each node having a list of neighbors. An adjacency list is used for the representation of a sparse graph.
What is an adjacency matrix?
An adjacency matrix is a square matrix with dimensions equivalent to the number of nodes in the graph. An adjacency matrix is preferred when the graph is dense.
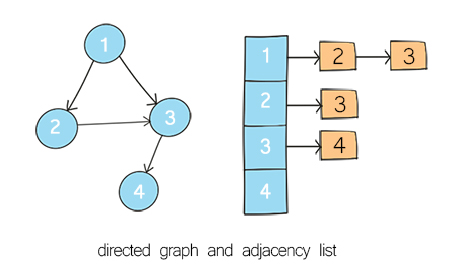
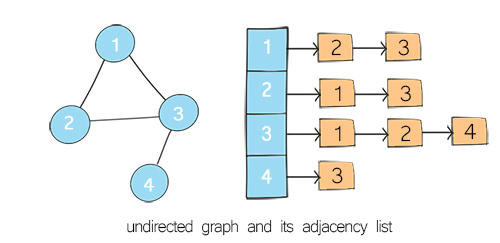
You are here

Part 1 – Graph as an adjacency list
Part 2 – Weighted graph as an adjacency list
Add node and edge
First, we define a Graph class. The Graph class has two fields: adj and directed. adj is a HashMap in which the key is the node, the value is all its neighbors. The value is represented as a linked list of neighbors. directed is a boolean variable to specify whether the graph is directed or undirected. By default, it is undirected.
In many old implementations of adjacency lists, adj is defined as an array of node lists. The disadvantage of this implementation is that we have to define the length of the array first. To avoid this, we use a hashmap. By using hashmap, we can retrieve the node and its neighbors by node itself, not by index in the array. Note the node can be any data type, such as Integer or String, or a customer-defined graphNode class.
To add a node to the graph is to add a key in the hashmap. To add an edge is to add an item in this key’s value. The following method addEdge includes both adding a node and adding an edge. For a directed graph, we add an edge from a to b. For the undirected graph, we also add an edge from b to a.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | import java.util.*; public class Graph<T> { Map<T, LinkedList<T>> adj = new HashMap<>(); boolean directed; //Constructor, Time O(1) Space O(1) public Graph() { directed = false; //default, Undirected graph } //Constructor, Time O(1) Space O(1) public Graph(boolean d) { directed = d; } //Add edges including adding nodes, Time O(1) Space O(1) public void addEdge(T a, T b) { adj.putIfAbsent(a, new LinkedList<>()); //add node adj.putIfAbsent(b, new LinkedList<>()); //add node adj.get(a).add(b); //add edge if (!directed) { //undirected adj.get(b).add(a); } } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | class Graph { //Constructor, Time O(1) Space O(1) constructor(directed) { this.adj = new Map(); this.directed = directed; //true or false } //Add edges including adding nodes, Time O(1) Space O(1) addEdge(a, b) { if (this.adj.get(a) == null) this.adj.set(a, new Array()); if (this.adj.get(b) == null) this.adj.set(b, new Array()); this.adj.get(a).push(b); if (!this.directed) this.adj.get(b).push(a); } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | class Graph: #Constructor, Time O(1) Space O(1) def __init__(self, directed): self.adj = {} self.directed = directed #true or false #Add edges including adding nodes, Time O(1) Space O(1) def addEdge(self, a, b): if a not in self.adj: self.adj[a] = [] if b not in self.adj: self.adj[b] = [] self.adj[a].append(b) if (self.directed == False): self.adj[b].append(a) |
Doodle

Remove node and edge
The removal operation can be removing an edge or removing a node. To remove an edge, we use the first node as the key to find its neighbors in the hashmap. Then remove the second node from its neighbors. For a directed graph, we just need to remove the edge from a to b. For an undirected graph, we also need to remove the edge from b to a.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Remove direct connection between a and b, Time O(1) Space O(1) public boolean removeEdge(T a, T b) { if (!adj.containsKey(a) || !adj.containsKey(b)) return false; //stop when input is invalid LinkedList<T> neighborsOfA = adj.get(a); LinkedList<T> neighborsOfB = adj.get(b); if (neighborsOfA == null || neighborsOfB == null) return false; //stop when no neighbors found boolean r1 = neighborsOfA.remove(b); if (!directed) { //undirected boolean r2 = neighborsOfB.remove(a); return r1 && r2; } return r1; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | //Remove direct connection between a and b, Time O(1) Space O(1) removeEdge(a, b) { if (this.adj.get(a) == null || this.adj.get(b) == null) return false; var ne1 = this.adj.get(a); var ne2 = this.adj.get(b); if (ne1 == null || ne2 == null) return false; var index = ne1.indexOf(b); if (index < 0) return false; ne1.splice(index, 1); if (!this.directed) { index = ne2.indexOf(a); if (index < 0 ) return false; ne2.splice(index, 1) } return true; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #Remove direct connection between a and b, Time O(1) Space O(1) def removeEdge(self, a, b): if a not in self.adj or b not in self.adj: return False ne1 = self.adj[a] ne2 = self.adj[b] if ne1 == None or ne2 == None: return False if b not in ne1: return False ne1.remove(b) if (self.directed == False): if a not in ne2: return False ne2.remove(a) return True |
Doodle

To remove a node, we have to remove all connected edges before removing the node itself. For an undirected graph, first, we get all the neighbors of the node. Then for each of its neighbors, remove itself from the value list. For a directed graph, we search all keys in the hashmap for their values and check whether this node exists in their neighbors. If it does, remove it. The last step is to remove the node as the key in the hashmap. Then this node is no longer in the hashmap’s key set.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | //Remove a node including all its edges, //Time O(V+E) Space O(1), V is number of nodes, E is number of edges public boolean removeNode(T a) { if (!adj.containsKey(a)) //invalid input return false; if (!directed) { //undirected LinkedList<T> neighbors = adj.get(a); for (T node: neighbors) adj.get(node).remove(a); } else { //directed for (T key: adj.keySet()) adj.get(key).remove(a); } adj.remove(a); return true; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | //Remove a node including all its edges, Time O(V+E) Space O(1) removeNode(a) { if (this.adj.get(a) == null) return false; if (!this.directed) { //undirected var ne1 = this.adj.get(a); for (let node of ne1) { let list = this.adj.get(node); let index = list.indexOf(a); if (index >= 0) list.splice(index, 1); } } else { //directed for (let entry of this.adj.entries()) { let list = entry[1]; let index = list.indexOf(a); if (index >= 0) list.splice(index, 1); } } this.adj.delete(a); return true; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #Remove a node including all its edges, #Time O(V+E) Space O(1), def removeNode(self, a): if a not in self.adj: return False if self.directed == False: #undirected ne1 = self.adj[a] for node in ne1: self.adj[node].remove(a) else: #directed for k, v in self.adj.items(): if a in v: v.remove(a) self.adj.pop(a) return True |
Doodle

Search by node and edge
Search can be a search of a node, an edge, or a path. We can check whether there is a node existing in the graph. This can be done by simply checking if the hashmap contains the key. We can also check whether there is a direct connection between two nodes (aka whether there is an edge). This can be done by checking whether the second node is in the first node’s neighbors.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | //Check whether there is node by its key, Time O(1) Space O(1) public boolean hasNode(T key) { return adj.containsKey(key); } //Check whether there is direct connection between two nodes, Time O(1), Space O(1) public boolean hasEdge(T a, T b) { if (!adj.containsKey(a) || !adj.containsKey(b) ) return false; LinkedList<T> ne1 = adj.get(a); if (directed) //directed return ne1.contains(b); else { //undirected or bi-directed LinkedList<T> ne2 = adj.get(b); return ne1.contains(b) && ne2.contains(a); } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | //Check whether there is node with the key, Time O(1) Space O(1) hasNode(key) { return this.adj.has(key); } //Check whether there is direct connection between two nodes, Time O(1), Space O(1) hasEdge(a, b) { if (this.adj.get(a) == null || this.adj.get(b) == null) return false; var ne1 = this.adj.get(a); if (this.directed) //directed return ne1.includes(b); else { //undirected or bi-directed var ne2 = this.adj.get(b); return ne1.includes(b) && ne2.includes(a); } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #Check whether there is node by its key, Time O(1) Space O(1) def hasNode(self, key): return key in self.adj.keys() #Check whether there is direct connection between two nodes, Time O(1), Space O(1) def hasEdge(self, a, b): if a not in self.adj or b not in self.adj: return False ne1 = [] ne2 = [] if a in self.adj: ne1 = self.adj[a] if self.directed: #directed return b in ne1 else: #undirected or bi-directed if b in self.adj: ne2 = self.adj[b] return b in ne1 and a in ne2 |
Doodle

Find path with depth first search in graph
A more useful operation is to search for a path. A path is a sequence of edges. There can be more than one path between two nodes. There are two common approaches: depth first search (DFS) and breadth first search (BFS). In this section, we use DFS and BFS to find out whether there is a path from one node to another.
Depth First Search starts from the source node and explores the adjacent nodes as far as possible before returning. DFS is usually implemented with recursion or stack. It is used to solve find-path or detect cycle problems.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | //Check there is path from src and dest //DFS, Time O(V+E), Space O(V) public boolean dfsHasPath(T src, T dest) { if (!adj.containsKey(src) || !adj.containsKey(dest)) return false; HashMap<T, Boolean> visited = new HashMap<>(); return dfsHelper(src, dest, visited); } //DFS helper, Time O(V+E), Space O(V) private boolean dfsHelper(T v, T dest, HashMap<T, Boolean> visited) { if (v == dest) return true; visited.put(v, true); for (T ne : adj.get(v)) { if (visited.get(ne) == null) return dfsHelper(ne, dest, visited); } return false; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | //Check there is path from src and dest //DFS, Time O(V+E), Space O(V) dfs(src, dest) { if (this.adj.get(src) == null || this.adj.get(dest) == null) return false; var visited = new Map(); return this.dfsHelper(src, dest, visited); } //DFS helper, Time O(V+E), Space O(V) dfsHelper(v, dest, visited) { if (v == dest) return true; visited.set(v, true); for (let ne of this.adj.get(v)) { if (visited.get(ne) == null) return this.dfsHelper(ne, dest, visited); } return false; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | # Check there is path from src and dest # DFS, Time O(V+E), Space O(V) def dfs(self, src, dest): if src not in self.adj or dest not in self.adj: return False visited = {} return self.dfsHelper(src, dest, visited) #DFS helper, Time O(V+E), Space O(V) def dfsHelper(self, v, dest, visited): if v == dest: return True visited[v] = True for ne in self.adj[v]: if ne not in visited: return self.dfsHelper(ne, dest, visited) return False |
Doodle

Find path with breadth first search in graph
Breath First Search starts from the source node and explores all its adjacent nodes before going to the next level of adjacent nodes. BFS is usually implemented with a queue. It is often used to solve shortest-path problems.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | //Check there is path from src and dest //BFS, Time O(V+E), Space O(V), V is number of vertices, E is number of edges public boolean bfsHasPath(T src, T dest) { if (!adj.containsKey(src) || !adj.containsKey(dest)) return false; HashMap<T, Boolean> visited = new HashMap<>(); Queue<T> q = new LinkedList<>(); visited.put(src, true); q.add(src); while (!q.isEmpty()) { T v = q.poll(); for (T ne : adj.get(v)) { if (ne == dest) return true; if (visited.get(ne) == null) { q.add(ne); visited.put(ne, true); } } } return false; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | //Check there is path from src and dest //BFS, Time O(V+E), Space O(V), V is number of vertices, E is number of edges bfs(src, dest) { if (this.adj.get(src) == null || this.adj.get(dest) == null) return false; var visited = new Map(); var q = new Array(); visited.set(src, true); q.push(src); while (q.length > 0) { let v = q.shift(); for (let ne of this.adj.get(v)) { if (ne == dest) return true; if (visited.get(ne) == null) { q.push(ne); visited.set(ne, true); } } } return false; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #Check there is path from src and dest #BFS, Time O(V+E), Space O(V) def bfs(self, src, dest): if src not in self.adj or dest not in self.adj: return False visited = {} q = [] visited[src] = True q.append(src) while q: v = q.pop(0) for ne in self.adj[v]: if ne == dest: return True if ne not in visited: q.append(ne) visited[ne] = True return False |
Print graph as adjacency list
The print operation is to display all nodes and their neighbors. Since it is a hashmap, you can print all keys and entries in the hashmap. This method is used for debugging purposes.
Java
1 2 3 4 5 6 | //Print graph as hashmap, Time O(V+E), Space O(1) public void print() { for (T key: adj.keySet()) { System.out.println(key + "," + adj.get(key)); } } |
JavaScript
1 2 3 4 5 6 | //Print graph as hashmap, Time O(V+E), Space O(1) print() { for (let entry of this.adj.entries()) { console.log(entry[0] + "-" + entry[1]); } } |
Python
1 2 3 4 | # Print graph as hashmap, Time O(V+E), Space O(1) def printGraph(self) : for k, v in self.adj.items(): print(str(k) + "-" + str(v)) |
Traverse with depth first search in graph
DFS traversal is to use depth-first search to visit nodes in the graph and print the node’s information. This is similar to DFS traversal in a binary tree. Starting from the source node, we call the recursive method to visit one of its neighbors, then a neighbor of the neighbor, and so on. Please note the source node might be any node in the graph. Some nodes might not be reached in a directed graph. (In a binary tree, we always start from the root and all nodes should be visited.)
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | //Traversal starting from src, DFS, Time O(V+E), Space O(V) public void dfsTraversal(T src) { if (!adj.containsKey(src)) return; HashMap<T, Boolean> visited = new HashMap<>(); helper(src, visited); System.out.println(); } //DFS helper, Time O(V+E), Space O(V) private void helper(T v, HashMap<T, Boolean> visited) { visited.put(v, true); System.out.print(v.toString() + " "); for (T ne : adj.get(v)) { if (visited.get(ne) == null) helper(ne, visited); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | //Traversal starting from src, DFS, Time O(V+E), Space O(V) dfsTraversal(src) { if (this.adj.get(src) == null) return; var visited = new Map(); this.helper(src, visited); } //DFS helper, Time O(V+E), Space O(V) helper(v, visited) { visited.set(v, true); console.log(v.toString()); for (let ne of this.adj.get(v)) { if (visited.get(ne) == null) this.helper(ne, visited); } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #Traversal starting from src, DFS, Time O(V+E), Space O(V) def dfsTraversal(self, src): if src not in self.adj: return visited = {} self.helper(src, visited) #DFS helper, Time O(V+E), Space O(V) def helper(self, v, visited): visited[v] = True print(str(v)) for ne in self.adj[v]: if ne not in visited: self.helper(ne, visited) |
Doodle

Traverse with breadth first search in graph
BFS traversal is to use breadth-first search to visit all nodes in the graph and print the node’s information. This is similar to BFS traversal in a binary tree. Starting from the source node, visit all its neighbors first before visiting the next level of neighbors. Please note the source might be any node in the graph. Some nodes might not be reached in a directed graph. (In a binary tree, we always start from the root and all nodes should be visited.)
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | //Traversal starting from src, BFS, Time O(V+E), Space O(V) public void bfsTraversal(T src) { if (!adj.containsKey(src)) return; Queue<T> q = new LinkedList<>(); HashMap<T, Boolean> visited = new HashMap<>(); q.add(src); visited.put(src, true); while (!q.isEmpty()) { T v = q.poll(); System.out.print(v.toString() + " "); for (T ne : adj.get(v)) { if (visited.get(ne) == null) { q.add(ne); visited.put(ne, true); } } } System.out.println(); } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | //Traversal starting from src, BFS, Time O(V+E), Space O(V) bfsTraversal(src) { if (this.adj.get(src) == null) return; var q = new Array(); var visited = new Map(); q.push(src); visited.set(src, true); while (q.length > 0) { let v = q.shift(); console.log(v.toString() + " "); for (let ne of this.adj.get(v)) { if (visited.get(ne) == null) { q.push(ne); visited.set(ne, true); } } } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | # Traversal starting from src, BFS, Time O(V+E), Space O(V) def bfsTraversal(self, src): if src not in self.adj: return q = [] visited = {} q.append(src) visited[src] = True while (len(q) > 0): v = q.pop(0) print(str(v) + " ") for ne in self.adj[v]: if ne not in visited: q.append(ne) visited[ne] = True |
Doodle

Free download
Download Graph implementation in Java, JavaScript and Python
Data structures introduction PDF