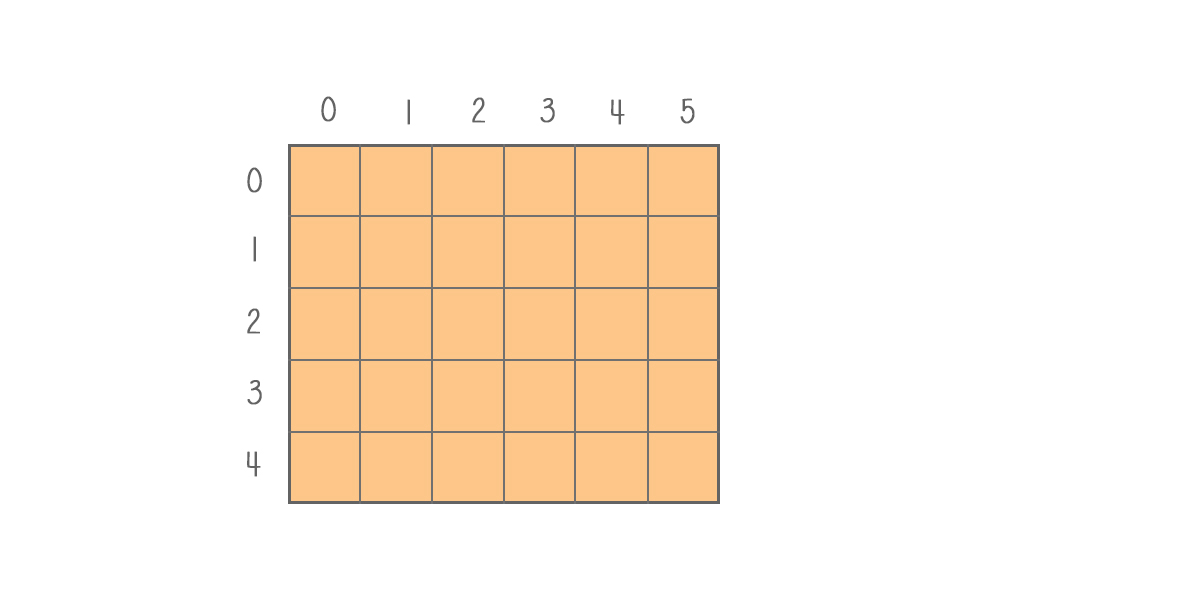
A matrix is a two-dimensional or 2d array. The number of rows and the number of columns should be defined when it is declared. The element in the matrix can be assigned and updated by the index of the row and column, as matrix[r][c]. Here is the implementation of matrix operations – initialize, update, search, and traversal.
Map of array implementations
Part 1 – array implementation
Part 2 – sorted array implementation
Part 3 – 2d array implementation
Table of Content
Initialize values in a 2d array
Matrix can be initialized by assigning single value with index of the row and the column. It can also be initialized by coping from another matrix. When copying from another matrix, a nested for loops will be used to iterate through all elements.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | public class Matrix<T extends Comparable<T>> { private T[][] board; private int rows, columns; //constructor, Time O(m*n), Space O(m*n), //m is number of rows, n is length of number of columns @SuppressWarnings("unchecked") public Matrix(T[][] input) { rows = input.length; columns = input[0].length; board = (T[][]) new Comparable[rows][columns]; for (int i = 0; i < rows; i++) { board[i] = Arrays.copyOf(input[i], columns); } } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | class Matrix { //constructor, Time O(m*n), Space O(m*n), //m is number of rows, n is length of number of columns constructor(input) { this.rows = input.length; this.columns = input[0].length; this.board = []; for (let i = 0; i < this.rows; i++) { this.board[i] = []; for (let j = 0; j < this.columns; j++) { this.board[i][j] = input[i][j]; } } } } |
Python
1 2 3 4 5 6 7 8 9 10 | class Matrix : #constructor, Time O(m*n), Space O(m*n), #m is number of rows, n is length of number of columns def __init__(self, input) : self.rows = len(input) self.columns = len(input[0]) self.matrix = [[0 for j in range(self.columns)] for i in range(self.rows)] for i in range (0, self.rows): for j in range(0, self.columns): self.matrix[i][j] = input[i][j] |
Update
To update a value is to assign a new value at the index of row and column.
Java
1 2 3 4 | //Time O(1), Space O(1) public void update(int r, int c, T value) { board[r][c] = value; } |
Javascript
1 2 3 4 | //Time O(1), Space O(1) update(r, c, value) { this.board[r][c] = value; } |
Python
1 2 3 | #Time O(1), Space O(1) def update_cell(self, r, c, value) : self.matrix[r][c] = value |
Search
There are two ways to search. If the matrix is not sorted, we can scan the elements one by one and rows by rows. If the matrix is sorted horizontally and vertically, we can use two pointers technique to search.
Initialize one pointer pointing to the first row, and the second pointer pointing to the last column. When the element is larger than the key, decrease the column. If the element is less than the key, increase the row. Eventually, the element will be found. This way, the time complexity improves from O(m*n) to O(m+n).
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | //Search in un-sorted matrix, Time O(m*n), Space O(1) public int[] searchMatrix(T key) { for (int i = 0; i < rows; i++) { for (int j = 0; j < columns; j ++) { if (board[i][j] == key) return new int[]{i, j}; } } return new int[]{-1,-1}; } //Search in sorted matrix, two pointers, Time O(m+n), Space O(1) public int[] searchSortedMatrix(T key) { int row = 0; int col = columns - 1; while (row < rows && col >= 0) { if (board[row][col] == key) { return new int[]{row,col}; } else if (board[row][col].compareTo(key) < 0) { row++; } else { col--; } } return new int[]{-1,-1}; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | //Search in un-sorted matrix, Time O(m*n), Space O(1) searchMatrix(key) { for (let i = 0; i < this.rows; i++) { for (let j = 0; j < this.columns; j ++) { if (this.board[i][j] == key) return [i, j]; } } return [-1,-1]; } //Search in sorted matrix, two pointers, Time O(m+n), Space O(1) searchSortedMatrix(key) { var row = 0; var col = this.columns - 1; while (row < this.rows && col >= 0) { if (this.board[row][col] == key) { return [row,col]; } else if (this.board[row][col] < key) { row++; } else { col--; } } return [-1,-1]; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #Search in un-sorted matrix, Time O(m*n), Space O(1) def search_matrix(self, key) : for i in range(0, self.rows) : for j in range (0, self.columns): if self.matrix[i][j] == key: return [i, j] return [-1,-1] #Search in sorted matrix, two pointers, Time O(m+n), Space O(1) def search_sorted_matrix(self, key): row = 0 col = len(self.matrix[0]) - 1 while row < self.rows and col >= 0: if (self.matrix[row][col] == key) : return [row,col] elif (self.matrix[row][col] < key) : row += 1 else : col -= 1 return [-1,-1] |
Doodle

Print
Print is to using two nested loops to print out all elements in the matrix.
Java
1 2 3 4 5 6 7 8 | //print matrix, Time O(m*n), Space O(1) public void printMatrix() { for (int i = 0; i < rows; i++) { for (int j = 0; j < columns; j ++) System.out.print( board[i][j] + " "); System.out.println(); } } |
Javascript
1 2 3 4 5 6 7 8 9 10 | //print matrix, Time O(m*n), Space O(1) printMatrix() { for (let i = 0; i < this.rows; i++) { var s = ''; for (let j = 0; j < this.columns; j ++) { s += this.board[i][j] + ' '; } console.log(s); } } |
Python
1 2 3 4 5 6 7 | #print matrix, Time O(m*n), Space O(1) def print_matrix(self): for i in range(0, self.rows) : s = '' for j in range (0, self.columns): s += str(self.matrix[i][j]) + ' ' print(s) |
Free download
Download Java, JavaScript and Python code
Data structures and Java collections
Can I use binary search in a sorted 2d array?
If a 2d array is sorted horizontally and is ascending row by row, you can use binary search. If a 2d array is sorted horizontally and vertically respectively, there might be an element in the last column larger than the first element in the next row. You cannot use binary search. Use a technique of two-pointers instead.