A min-heap is a complete binary tree where all levels, except the last level, are completely filled. There is no “hole” in the tree. A min-heap should meet these criteria: the parent’s value is less than both children’s values. The smallest value is at the root.
This post is the min-heap implementation. The max-heap is in opposite order. Note the search and traversal in the min-heap is the same as the max-heap, so please refer to the max-heap for these two operations.
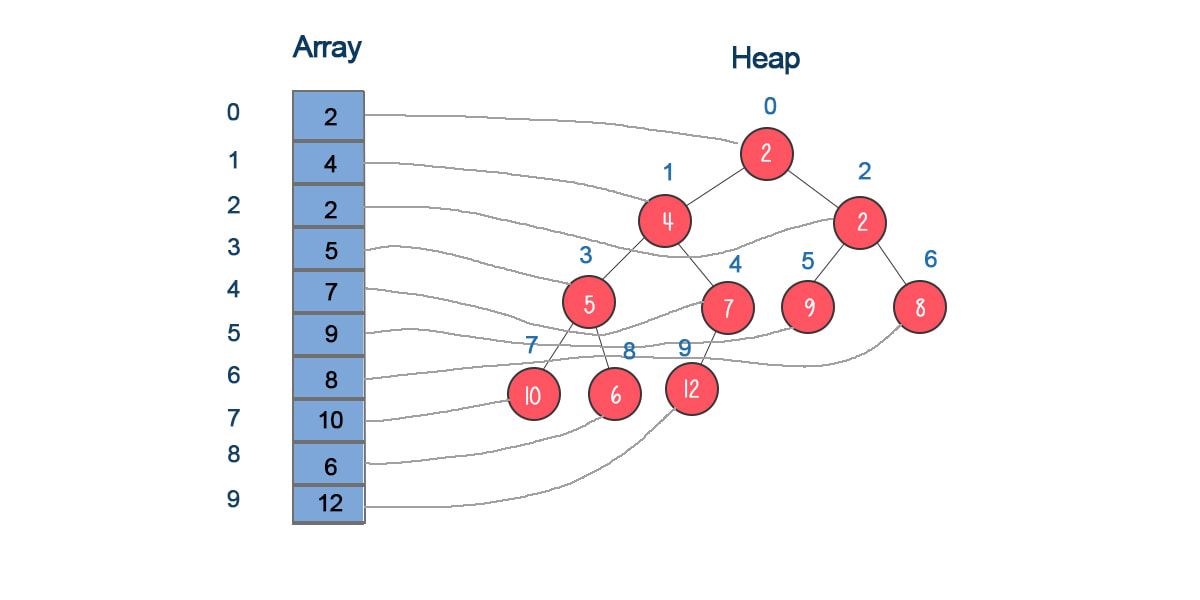
Table of Content
Map of heap implementations
Part 1 – Max-heap implementation
Part 2 – Min-heap implementation
Insert
We declare three attributes: heap, length, and maxSize. heap is an array. maxSize is the max length of the array. It is used to initialize the array. length is the actual number of elements in the array. It starts from 0.
To insert a new element, we put the new value at the end of the array. Then we move it up in the heap based on its value compared to its parent. If its value is less than its parent, it should be switched the position with its parent. We keep doing it until it is below a node with a smaller value and above one or two nodes with larger values. We call this process bubble up.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import java.util.*; public class MinHeap<T extends Comparable<T>> { T[] heap; int length; int maxSize; //Time O(1) Space O(1) @SuppressWarnings("unchecked") public MinHeap(int capacity) { maxSize = capacity; heap = (T[]) new Comparable[capacity]; length = 0; // means queue is empty } //Insert a new value, Time O(logn), Space O(1), n is number of items in heap public void insert(T value) { if (length == maxSize) { System.out.println("heap is full, cannot insert " + value); return; } heap[length]= value; bubbleUp(length); length++; } //Time O(logn), Space O(1) private void bubbleUp(int pos) { int parentPos = (pos-1)/2; T value = heap[pos]; while (pos > 0 && (value.compareTo(heap[parentPos]) < 0)) { heap[pos] = heap[parentPos]; pos = parentPos; parentPos= (parentPos-1)/2; } heap[pos] = value; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
class MinHeap { //Constructor, Time O(1) Space O(1) constructor(capacity) { this.maxSize = capacity; this.length = 0; this.heap = []; } //Insert a new value, Time O(logn), Space O(1), n is number of items in heap insert(value) { if (this.length >= this.maxSize) { console.log("heap is full, cannot insert"); return; } this.heap[this.length] = value; this.bubbleUp(this.length); this.length++; } //Time O(logn), Space O(1) bubbleUp(pos) { var parentPos = Math.floor((pos-1)/2); var value = this.heap[pos]; while (pos > 0 && value < this.heap[parentPos]) { this.heap[pos] = this.heap[parentPos]; pos = parentPos; parentPos= Math.floor((parentPos-1)/2); } this.heap[pos] = value; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
class MinHeap: # Time O(1) Space O(1) def __init__(self, capacity): self.maxSize = capacity self.length = 0 self.heap = [None]*capacity # Insert a new value, Time O(logn), Space O(1), n is number of items in heap def insert(self, value): if self.length >= self.maxSize: print("heap reach max size, return") return self.heap[self.length] = value # start from last self.bubble_up(self.length) self.length += 1 # Time O(logn), Space O(1) def bubble_up(self, pos): parentPos = int((pos-1)/2) value = self.heap[pos] while pos > 0 and value < self.heap[parentPos]: self.heap[pos] = self.heap[parentPos] pos = parentPos parentPos= int((parentPos-1)/2) self.heap[pos] = value |
Remove
The removal operation is to remove the element at the root, which has the smallest value. This is the first element in the underlying array. When we remove the first element in the array, we move the last element to the first to fill out the empty spot. But this element’s value might be larger than its children’s. To correct this, we compare its value with its children’s values and switch with the child with the smaller value. We keep doing it until it is below a node with a smaller value and above one or two nodes with larger values. This process is called bubble down. Bubble down is more complicated than bubble up because it has two children to compare.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//Remove from min (first one), Time O(logn), Space O(1) public T remove() { if (length == 0) { System.out.println("heap is empty"); return null; } T min = heap[0]; heap[0] = heap[length-1]; //last put first length--; bubbleDown(0); return min; } //Time O(logn), space O(1) private void bubbleDown(int pos) { T item = heap[pos]; int index; while (pos < length/2) { int left = 2*pos + 1; int right = 2*pos + 2; if (right < length && heap[left].compareTo(heap[right]) > 0) index = right; else index = left; if (item.compareTo(heap[index]) <= 0) break; heap[pos] = heap[index]; pos = index; } heap[pos] = item; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//Remove from min (first one), Time O(logn), Space O(1) remove() { if (this.length == 0) { console.log("heap is empty"); return null; } var min = this.heap[0]; this.heap[0] = this.heap[this.length-1]; //put last at first this.length--; this.bubbleDown(0); return min; } //Time O(logn), Space O(1) bubbleDown(pos) { var item = this.heap[pos]; var index; while (pos < Math.floor(this.length/2)) { let left = 2*pos + 1; let right = 2*pos + 2; if (right < this.length && this.heap[left] > this.heap[right]) index = right; else index = left; if (item <= this.heap[index]) break; this.heap[pos] = this.heap[index]; pos = index; } this.heap[pos] = item; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# Remove from min (first one), Time O(logn), Space O(1) def remove(self): if self.length == 0: print("heap is empty") return None min = self.heap[0] self.heap[0] = self.heap[self.length-1] # put the last at first self.length -= 1 self.bubble_down(0) return min # Time O(logn), Space O(1) def bubble_down(self, pos): item = self.heap[pos] index = 0 while pos < int(self.length/2): left = 2*pos + 1 right = 2*pos + 2 if right < self.length and self.heap[left] > self.heap[right]: index = right else: index = left if item <= self.heap[index]: break self.heap[pos] = self.heap[index] pos = index self.heap[pos] = item |
Free download
Download Min-heap implementation in Java, JavaScript and Python
Data structures introduction
What is the time complexity of insertion and deletion in a heap?
Since the heap is a complete binary tree, the time complexity is O(logn).
What is a min-heap?
A min-heap is a complete binary tree where all levels, except the last level, are completely filled. There is no “hole” in the tree. A min-heap should meet these criteria: the parent’s value is less than both children’s values. The smallest value is at the root.