Priority queue implementation provides code to implement priority queue using unordered array. A priority queue is a queue in which we insert an element at the back (enqueue) and remove an element from the front (dequeue). The element with the highest priority shall be dequeued first. This post is using unordered array. In enqueue, the time complexity is O(1). In dequeue, the time complexity is O(n).
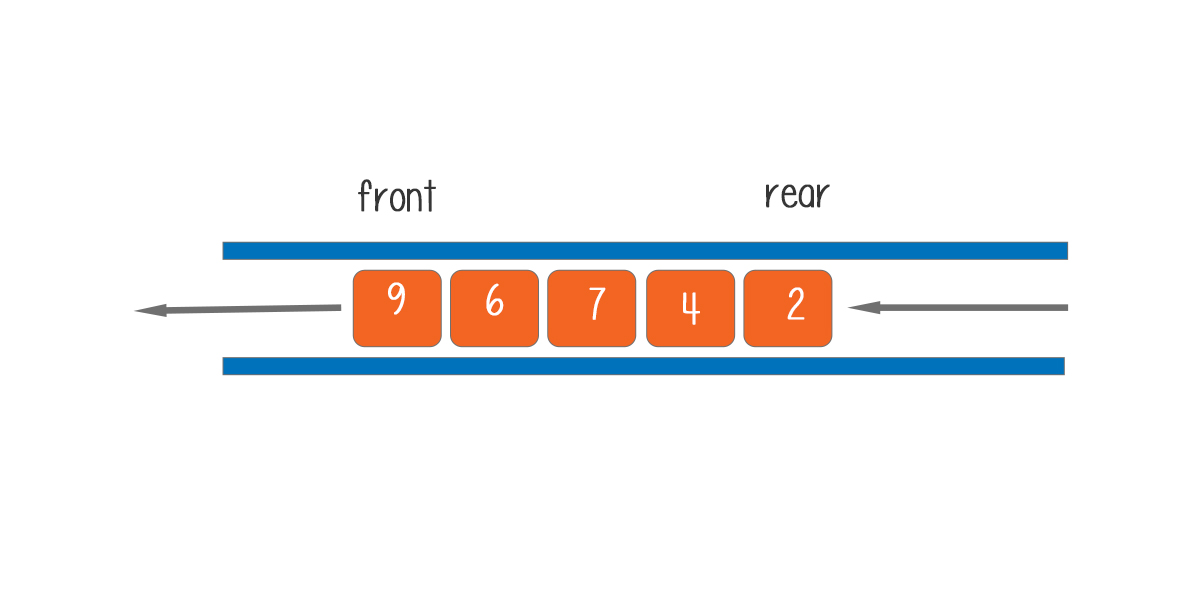
Table of Content
Map of priority queue implementations
Part 1 – priority queue implementation – ordered array
Part 2 – priority queue implementation – unordered array
Part 3 – priority queue implementation with heap – iterative solution
Part 4 – priority queue implementation with heap – recursive solution
Enqueue in priority queue implementation
To enqueue an element is the same as adding an element in a regular array -add the element at next available spot in the array (ie at the end).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
// Descending priority, the higher the key, the higher the priority @SuppressWarnings({"unchecked"}) public class PriorityQueueArray2<T extends Comparable<T>> { private T[] pqArray; private int length; private int maxSize; public PriorityQueueArray2(int capacity) { maxSize = capacity; pqArray = (T[])new Comparable[capacity]; } //Add at the end without sorting, Time O(1), Space O(1), public void enqueue(T value ) { if(length == maxSize) { System.out.println("The priority queue is full! can not enqueue " + value); return; } pqArray[length] = value; length++; } } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
//Descending priority, the higher the key, the higher the priority class PriorityQueueArrayUnordered { //Constructor, Time O(1), Space O(1) constructor(capacity) { this.maxSize = capacity; this.pqArray = {}; this.length = 0; } //Add at the end without sorting, Time O(1), Space O(1), enqueue(value) { if (this.length == this.maxSize) { console.log("priority queue is full, cannot enqueue " + value); return; } this.pqArray[this.length] = value; this.length++; } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# Descending priority, the higher the key, the higher the priority class PriorityQueueArrayUnordered: # Constructor, Time O(1), Space O(1) def __init__(self, capacity) : self.maxSize = capacity self.pqArray = {} self.length = 0 # Add at the end without sorting, Time O(1), Space O(1) def enqueue(self, value) : if (self.length == self.maxSize) : print("priority queue is full, cannot enqueue " + str(value)) return self.pqArray[self.length] = value self.length += 1 |
Doodle
Dequeue
The dequeue operation is to remove the highest priority element from the array. Since the array is not ordered, we have to find the highest priority element first. This requires to exam all elements in the array. Then move the last element in the array to this spot to replace (remove) it. This time complexity is O(n).
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
//Find the biggest and delete it, Time O(n), Space O(1) public T dequeue() { if (length == 0) { System.out.println("The priority queue is empty! can not dequeue."); return null; } int maxIndex = 0; for (int i = 1; i < length; i++) { //search for biggest if (pqArray[i].compareTo (pqArray[maxIndex]) > 0) { maxIndex = i; } } T item = pqArray[maxIndex]; System.out.println("dequeue: " + item); length--; pqArray[maxIndex] = pqArray[length]; //move the last to this spot return item; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
//Find the biggest and delete it, Time O(n), Space O(1) dequeue() { if (this.length == 0) { console.log("queue is empty"); return null; } var maxIndex = 0; for (let i = 1; i < this.length; i++) { //search for biggest if (this.pqArray[i] > this.pqArray[maxIndex]) { maxIndex = i; } } var item = this.pqArray[maxIndex]; this.length--; this.pqArray[maxIndex] = this.pqArray[this.length]; //move the last to this spot return item; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# Find the biggest and delete it, Time O(n), Space O(1) def dequeue(self) : if (self.length == 0 ) : print("queue is empty") return None maxIndex = 0 for i in range(1, self.length): #search for biggest if (self.pqArray[i] > self.pqArray[maxIndex]) : maxIndex = i; item = self.pqArray[maxIndex]; self.length -= 1 self.pqArray[maxIndex] = self.pqArray[self.length]; #move the last to this spot return item |
Peek
Peek is to return the value of the highest priority element. The same as dequeue, we have to find the highest priority element by examing all elements in the array.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
//Find the biggest and return it, Time O(n), Space O(1) public T peek() { if (length == 0){ System.out.println("The priority queue is empty!"); return null; } int maxIndex = 0; for (int i = 1; i < length; i++) { //search for biggest if (pqArray[i].compareTo (pqArray[maxIndex]) > 0) { maxIndex = i; } } return pqArray[maxIndex]; } |
Javascript
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
//Find the biggest and return it, Time O(n), Space O(1) peek() { if (tthis.length == 0) { console.log("queue is empty"); return null; } var maxIndex = 0; for (let i = 1; i < this.length; i++) { //search for biggest if (this.pqArray[i] > this.pqArray[maxIndex]) { maxIndex = i; } } return this.pqArray[maxIndex]; } |
Python
|
1 2 3 4 5 6 7 8 9 10 |
#Find the biggest and return it, Time O(n), Space O(1) def peek(self) : if (self.length == 0) : print("queue is empty") return None maxIndex = 0 for i in range(1, self.length): #search for biggest if (self.pqArray[i] > self.pqArray[maxIndex]) : maxIndex = i; return self.pqArray[maxIndex] |
Print
Print is to print all elements in the array, starting from the index 0 to highest index. A for loop is used to iterate through each element.
Java
|
1 2 3 4 5 6 7 |
//print all, in insert order, Time O(n), Space O(1) public void print() { System.out.print("Priority Queue: "); for (int i = 0; i < length; i++) System.out.print(pqArray[i] + " "); System.out.println(); } |
Javascript
|
1 2 3 4 5 6 7 |
//print all, in insert order, Time O(n), Space O(1) print() { var line = "Priority Queue: "; for (let i = 0; i < this.length; i++) line += this.pqArray[i] + " "; console.log(line); } |
Python
|
1 2 3 4 5 6 |
# print all, in insert order, Time O(n), Space O(1) def print(self) : line = "Priority Queue: " for i in range (0, self.length): line += str(self.pqArray[i]) + " " print(line) |
Free download
Download priority queue implementation with array in Java, JavaScript and Python
Data structures introduction PDF
How to implement a priority queue using an array?
There are two ways to implement priority queue using an array. The first is to implement as an ordered array. All element are sorted during insertion. The second way is to allow new element to enter as a regular array. When dequeue, find the highest priority element by checking all elements.