A graph is a data structure that consists of a set of nodes connected by edges. Graphs are used to simulate many real-world problems, such as routes in cities, circuit networks, and social networks. This is graph implementation part 2 – weighted graph as an adjacency list.

Table of Content
- Terminology
- Map of graph implementations
- Define classes
- Add node and edge
- Remove node and edge
- Search by node and edge
- Find path with DFS in weighted graph
- Find path with BFS in weighted graph
- Print weighted graph as adjacency list
- Traverse with DFS in weighted graph
- Traverse with BFS in weighted graph
- Free download
Terminology
A node in the graph is also called a vertex. A line between two nodes is an edge. Two nodes are adjacent, called neighbors if they are connected through an edge. A path represents a sequence of edges between the two nodes.
In a directed graph, all of the edges represent a one-way relationship. In an undirected graph, all edges are bidirectional.
If the edges in the graph have weights, the graph is said to be a weighted graph. If the edges do not have weights, the graph is said to be unweighted.
The weight of the edges might represent the distances between two cities, or the cost of flights, etc. The problems such as finding the shortest path or longest path are applied to weighted graphs.
Weighted graphs can be directed or undirected. For example, the minimum spanning tree is an undirected graph. The Dijkstra’s algorithm to find the shortest path is for directed graphs.
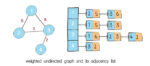
A graph can be presented as an adjacency list or adjacency matrix. An adjacency list is a “list of lists”, i.e. a list of nodes, with each node having a list of neighbors. An adjacency list is used for the representation of a sparse graph. An adjacency matrix is a square matrix with dimensions equivalent to the number of nodes in the graph. An adjacency matrix is preferred when the graph is dense.


Map of graph implementations
Part 1 – Graph implementation as adjacency list

Part 2 – Weighted graph as adjacency list
Part 3 – Depth first search in an adjacency matrix
Part 4 – Shortest path in an adjacency matrix
Define classes
First, we define an Edge class. It has two fields: neighbor and weight. The neighbor is the node at the other end of the edge. weight is the value associated with the edge.
The GraphWeighted class has two fields: adj and directed. adj is a HashMap with nodes as keys and linked lists of edges as values. directed is a boolean variable to specify whether the graph is directed or undirected. By default, it is undirected.
The nodes can be any data type, such as Integer or String, or a customer-defined graphNode class.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | import java.util.*; class Edge<T> { T neighbor; //connected vertex int weight; //weight //Constructor, Time O(1) Space O(1) public Edge(T v, int w) { this.neighbor = v; this.weight = w; } //Time O(1) Space O(1) @Override public String toString() { return "(" + neighbor + "," + weight + ")"; } } public class WeightedGraph<T> { Map<T, LinkedList<Edge<T>>> adj = new HashMap<>(); boolean directed; //Constructor, Time O(1) Space O(1) public WeightedGraph () { directed = false; //default, Undirected graph } //Constructor, Time O(1) Space O(1) public WeightedGraph(boolean d) { directed = d; } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | class Edge { //Constructor, Time O(1) Space O(1) constructor(v, w) { this.neighbor = v; this.weight = w; } //Time O(1) Space O(1) toString() { return "(" + this.neighbor + "," + this.weight + ")"; } } class WeightedGraph { //Constructor, Time O(1) Space O(1) constructor(directed) { this.adj = new Map(); this.directed = directed; //true or false } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | class Edge: #Constructor, Time O(1) Space O(1) def __init__(self, v, w): self.neighbor = v self.weight = w #Time O(1) Space O(1) def __str__(self): return "(" + str(self.neighbor) + "," + str(self.weight) + ")" class WeightedGraph: #Constructor, Time O(1) Space O(1) def __init__(self, directed): self.adj = {} self.directed = directed #true or false |
Add node and edge
To add a node to the graph is to add a key in the hashmap. To add an edge is to add an item in this key’s value. The following method addEdge includes both adding a node and adding an edge. For a directed graph, we add an edge from a to b. For an undirected graph, we also add an edge from b to a. Note the weight is one of the inputs to create the edge object.
Java
1 2 3 4 5 6 7 8 9 10 11 | //Add edges including adding nodes, Time O(1) Space O(1) public void addEdge(T a, T b, int w) { adj.putIfAbsent(a, new LinkedList<>()); //add node adj.putIfAbsent(b, new LinkedList<>()); //add node Edge<T> edge1 = new Edge<>(b, w); adj.get(a).add(edge1); //add edge if (!directed) { //undirected Edge<T> edge2 = new Edge<>(a, w); adj.get(b).add(edge2); } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 | //Add edges including adding nodes, Time O(1) Space O(1) addEdge(a, b, w) { if (this.adj.get(a) == null) this.adj.set(a, new Array()); //add node if (this.adj.get(b) == null) this.adj.set(b, new Array()); //add node var edge1 = new Edge(b, w); this.adj.get(a).push(edge1); //add edge if (!this.directed) { let edge2 = new Edge(a, w); this.adj.get(b).push(edge2); //add edge } } |
Python
1 2 3 4 5 6 7 8 9 10 11 | #Add edges including adding nodes, Time O(1) Space O(1) def addEdge(self, a, b, w): if a not in self.adj: self.adj[a] = [] if b not in self.adj: self.adj[b] = [] edge1 = Edge(b, w) self.adj[a].append(edge1) if (self.directed == False): edge2 = Edge(a, w) self.adj[b].append(edge2) |
Remove node and edge
The removal operation can be removing an edge or removing a node. Before we continue, let’s create a utility method to find the edge between two nodes. Use one node as a key to find its neighbors. Then loop through the neighbors to find the other node. Return the first matched edge. This method will be used in the following operations.
To remove an edge, we use the node as the key to find its neighbors in the hashmap. Then remove the other node from its neighbors. For a directed graph, we need to remove the edge from a to b. For an undirected graph, we also need to remove the edge from b to a.
To remove a node, we have to remove all connected edges before removing the node itself. For an undirected graph, first, we get all the neighbors of the node. Then for each of its neighbors, remove itself from the value list. For a directed graph, we search all keys in the hashmap for their values and check whether this node exists in their neighbors. If it does, remove it. The last step is to remove the node as the key in the hashmap. Then this node is no longer in the hashmap’s key set.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | //Find the edge between two nodes, Time O(n) Space O(1), n is number of neighbors private Edge<T> findEdgeByNodes(T a, T b) { if (!adj.containsKey(a) || !adj.containsKey(b)) //invalid input return null; LinkedList<Edge<T>> ne = adj.get(a); for (Edge<T> edge: ne) { if (edge.neighbor.equals(b)) { return edge; } } return null; } //Remove direct connection between a and b, Time O(n) Space O(1) public boolean removeEdge(T a, T b) { if (!adj.containsKey(a) || !adj.containsKey(b)) //invalid input return false; LinkedList<Edge<T>> ne1 = adj.get(a); LinkedList<Edge<T>> ne2 = adj.get(b); if (ne1 == null || ne2 == null) return false; Edge<T> edge1 = findEdgeByNodes(a, b); if (edge1 == null) return false; ne1.remove(edge1); if (!directed) {//undirected Edge<T> edge2 = findEdgeByNodes(b, a); if (edge2 == null) return false; ne2.remove(edge2); } return true; } //Remove a node including all its edges, Time O(V+E) Space O(1), //V is number of nodes, E is number of edges public boolean removeNode(T a) { if (!adj.containsKey(a)) //invalid input return false; if (!directed) { //undirected LinkedList<Edge<T>> ne1 = adj.get(a); for (Edge<T> edge: ne1) { Edge<T> edge1 = findEdgeByNodes(edge.neighbor, a); adj.get(edge.neighbor).remove(edge1); } } else { //directed for (T key: adj.keySet()) { Edge<T> edge2 = findEdgeByNodes(key, a); if (edge2 != null) adj.get(key).remove(edge2); } } adj.remove(a); return true; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | //Find the edge between two nodes, Time O(n) Space O(1), n is number of neighbors findEdgeByNodes(a, b) { if (this.adj.get(a) == null || this.adj.get(b) == null) return -1; var ne = this.adj.get(a); for (let i = 0; i < ne.length; i++) { if (ne[i].neighbor == b) { return i; } } return -1; } //Remove direct connection between a and b, Time O(n) Space O(1) removeEdge(a, b) { if (this.adj.get(a) == null || this.adj.get(b) == null) return false; var ne1 = this.adj.get(a); var ne2 = this.adj.get(b); if (ne1 == null || ne2 == null) return false; var index1 = this.findEdgeByNodes(a, b); if (index1 < 0) return false; ne1.splice(index1, 1); if (!this.directed) { //undirected var index2 = this.findEdgeByNodes(b, a); if (index1 < 0) return false; ne2.splice(index2, 1) } return true; } //Remove a node including all its edges, //Time O(V+E) Space O(1) removeNode(a) { if (this.adj.get(a) == null) return false; if (!this.directed) { //undirected var ne1 = this.adj.get(a); for (let edge of ne1) { let list = this.adj.get(edge.neighbor); let index1 = this.findEdgeByNodes(edge.neighbor, a); if (index1 >= 0) list.splice(index1, 1); } } else { //directed for (let entry of this.adj.entries()) { let list = entry[1]; let index2 = this.findEdgeByNodes(entry[0], a); if (index2 >= 0) list.splice(index2, 1); } } this.adj.delete(a); return true; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | #Find the edge between two nodes, Time O(n) Space O(1), n is number of neighbors def findEdgeByNodes(self, a, b): if a not in self.adj or b not in self.adj: return None ne = self.adj.get(a) for edge in ne: if edge.neighbor == b: return edge return None #Remove direct connection between a and b, Time O(n) Space O(1) def removeEdge(self, a, b): if a not in self.adj or b not in self.adj: return False ne1 = self.adj[a] ne2 = self.adj[b] if ne1 == None or ne2 == None: return False edge1 = self.findEdgeByNodes(a, b) if edge1 == None: return False ne1.remove(edge1) if (self.directed == False): edge2 = self.findEdgeByNodes(b, a) if edge2 == None: return False ne2.remove(edge2) return True #Remove a node including all its edges, #Time O(V+E) Space O(1) def removeNode(self, a): if a not in self.adj: return False if self.directed == False: #undirected ne1 = self.adj[a] for edge in ne1: edge1 = self.findEdgeByNodes(edge.neighbor, a) self.adj[edge.neighbor].remove(edge1) else: #directed for k, v in self.adj.items(): edge2 = self.findEdgeByNodes(k, a) if edge2 is not None: self.adj[k].remove(edge2) self.adj.pop(a) return True |
Search by node and edge
Search can be a search of a node, an edge, or a path. We can check whether there is a node existing in the graph. This can be done by simply checking the hashmap contains the key. We can also check whether there is a direct connection between two nodes (aka whether there is an edge). This can be done by checking whether the second node is in the first node’s neighbors.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | //Check whether there is node by its key, Time O(1) Space O(1) public boolean hasNode(T key) { return adj.containsKey(key); } //Check whether there is direct connection between two nodes, Time O(n), Space O(1) public boolean hasEdge(T a, T b) { Edge<T> edge1 = findEdgeByNodes(a, b); if (directed) {//directed return edge1 != null; } else { //undirected or bi-directed Edge<T> edge2 = findEdgeByNodes(b, a); return edge1 != null && edge2 != null; } } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | //Check whether there is node with the key, Time O(1) Space O(1) hasNode(key) { return this.adj.has(key); } //Check whether there is direct connection between two nodes, Time O(n), Space O(1) hasEdge(a, b) { var index1 = this.findEdgeByNodes(a, b) if (this.directed) //directed return index1 >= 0; else { //undirected or bi-directed var index2 = this.findEdgeByNodes(b, a) return index1 >= 0 && index2 >= 0; } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 | #Check whether there is node by its key, Time O(1) Space O(1) def hasNode(self, key): return key in self.adj.keys() #Check whether there is direct connection between two nodes, Time O(n), Space O(1) def hasEdge(self, a, b): edge1 = self.findEdgeByNodes(a, b) if self.directed: #directed return edge1 is not None else: #undirected or bi-directed edge2 = self.findEdgeByNodes(b, a) return edge1 is not None and edge2 is not None |
Find path with depth first search in weighted graph
A more useful operation is to search for a path. A path is a sequence of edges. There can be more than one path between two nodes. There are two common approaches: depth-first search (DFS) and breadth-first search (BFS). In this section, we use DFS and BFS to find out whether there is a path from one node to another.
Depth First Search starts from the source node and explores the adjacent nodes as far as possible before returning. DFS is usually implemented with recursion or stack. It is used to solve find-path or detect cycle problems.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | //Check if there is path from src and dest //DFS, Time O(V+E), Space O(V) public boolean dfsHasPath(T src, T dest) { if (!adj.containsKey(src) || !adj.containsKey(dest)) //invalid input return false; HashMap<T, Boolean> visited = new HashMap<>(); return dfsHelper(src, dest, visited); } //DFS helper, Time O(V+E), Space O(V) private boolean dfsHelper(T v, T dest, HashMap<T, Boolean> visited) { if (v == dest) return true; visited.put(v, true); for (Edge<T> edge : adj.get(v)) { T u = edge.neighbor; if (visited.get(u) == null) return dfsHelper(u, dest, visited); } return false; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | //Check there is path from src and dest //DFS, Time O(V+E), Space O(V) dfsHasPath(src, dest) { if (this.adj.get(src) == null || this.adj.get(dest) == null) return false; var visited = new Map(); return this.dfsHelper(src, dest, visited); } //DFS helper, Time O(V+E), Space O(V) dfsHelper(v, dest, visited) { if (v == dest) return true; visited.set(v, true); for (let edge of this.adj.get(v)) { let u = edge.neighbor; if (visited.get(u) == null) return this.dfsHelper(u, dest, visited); } return false; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | # Check there is path from src and dest # DFS, Time O(V+E), Space O(V) def dfsHasPath(self, src, dest): if src not in self.adj or dest not in self.adj: return False visited = {} return self.dfsHelper(src, dest, visited) #DFS helper, Time O(V+E), Space O(V) def dfsHelper(self, v, dest, visited): if v == dest: return True visited[v] = True for edge in self.adj[v]: u = edge.neighbor if u not in visited: return self.dfsHelper(u, dest, visited) return False |
Find path with breadth first search in weighted graph
Breath First Search starts from the source node and explores all its adjacent nodes before going to the next level of adjacent nodes. BFS is usually implemented with a queue. It is often used to solve shortest-path problems.
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | //Check if there is path from src and dest //BFS, Time O(V+E), Space O(V), V is number of vertices, E is number of edges public boolean bfsHasPath(T src, T dest) { if (!adj.containsKey(src) || !adj.containsKey(dest)) //invalid input return false; HashMap<T, Boolean> visited = new HashMap<>(); Queue<T> q = new LinkedList<>(); visited.put(src, true); q.offer(src); while (!q.isEmpty()) { T v = q.poll(); if (v == dest) { return true; } for (Edge<T> edge: adj.get(v)) { T u = edge.neighbor; if (visited.get(u) == null) { visited.put(u, true); q.offer(u); } } } return false; } |
Javascript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | //Check there is path from src and dest //BFS, Time O(V+E), Space O(V), V is number of vertices, E is number of edges bfsHasPath(src, dest) { if (this.adj.get(src) == null || this.adj.get(dest) == null) return false; var visited = new Map(); var q = new Array(); visited.set(src, true); q.push(src); while (q.length > 0) { let v = q.shift(); if (v == dest) return true; for (let edge of this.adj.get(v)) { let u = edge.neighbor; if (visited.get(u) == null) { q.push(u); visited.set(u, true); } } } return false; } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | #Check there is path from src and dest #BFS, Time O(V+E), Space O(V) def bfsHasPath(self, src, dest): if src not in self.adj or dest not in self.adj: return False visited = {} q = [] visited[src] = True q.append(src) while q: v = q.pop(0) if v == dest: return True for edge in self.adj[v]: u = edge.neighbor if u not in visited: q.append(u) visited[u] = True return False |
Print weighted graph as adjacency list
The print operation is to display all nodes and their connections in the graph. This method is used for debugging purposes. This can be done by looping through the key set of the hashmap and printing the entries in the neighbor list.
Java
1 2 3 4 5 6 | //Print graph as hashmap, Time O(V+E), Space O(1) public void printGraph() { for (T key: adj.keySet()) { System.out.println(key + "," + adj.get(key)); } } |
JavaScript
1 2 3 4 5 6 | //Print graph as hashmap, Time O(V+E), Space O(1) printGraph() { for (let entry of this.adj.entries()) { console.log(entry[0] + "-" + entry[1]); } } |
Python
1 2 3 4 5 6 7 | # Print graph as hashmap, Time O(V+E), Space O(1) def printGraph(self): for k, v in self.adj.items(): print(str(k) + "-", end = "") for edge in v: print(edge, end = "") print() |
Traverse with depth first search in weighted graph
DFS traversal is to use depth-first search to visit all nodes in the graph and print the node’s information. This is similar to DFS traversal in a binary tree. Starting from the source node, we call the recursive method to visit one of its neighbors, and then a neighbor of the neighbor, and so on. Please note the source node might be any node in the graph. Some nodes might not be reached in a directed graph. (In a binary tree, we always start from the root and all nodes should be visited.)
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | //Traversal starting from src, DFS, Time O(V+E), Space O(V) public void dfsTraversal(T src) { if (!adj.containsKey(src)) //invalid input return; HashMap<T, Boolean> visited = new HashMap<>(); helper(src, visited); System.out.println(); } //DFS helper, Time O(V+E), Space O(V) private void helper(T v, HashMap<T, Boolean> visited) { visited.put(v, true); System.out.print(v.toString() + " "); for (Edge<T> edge : adj.get(v)) { T u = edge.neighbor; if (visited.get(u) == null) helper(u, visited); } } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | //Traversal starting from src, DFS, Time O(V+E), Space O(V) dfsTraversal(src) { if (this.adj.get(src) == null) return; var visited = new Map(); this.helper(src, visited); } //DFS helper, Time O(V+E), Space O(V) helper(v, visited) { visited.set(v, true); console.log(v.toString()); for (let edge of this.adj.get(v)) { let u = edge.neighbor; if (visited.get(u) == null) this.helper(u, visited); } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #Traversal starting from src, DFS, Time O(V+E), Space O(V) def dfsTraversal(self, src): if src not in self.adj: return visited = {} self.helper(src, visited) print() #DFS helper, Time O(V+E), Space O(V) def helper(self, v, visited): visited[v] = True print(str(v) + " ", end = "") for edge in self.adj[v]: u = edge.neighbor if u not in visited: self.helper(u, visited) |
Traverse with breadth first search in weighted graph
BFS traversal is to use breadth-first search to visit all nodes in the graph and print the node’s information. This is similar to BFS traversal in a binary tree. Starting from the source node, visit all its neighbors first before visiting the next level of neighbors. Please note the source node might be any node in the graph. Some nodes might not be reached in a directed graph. (In a binary tree, we always start from the root and all nodes should be visited.)
Java
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | //Traversal starting from src, BFS, Time O(V+E), Space O(V) public void bfsTraversal(T src) { if (!adj.containsKey(src)) //invalid input return; Queue<T> q = new LinkedList<>(); HashMap<T, Boolean> visited = new HashMap<>(); q.add(src); visited.put(src, true); while (!q.isEmpty()) { T v = q.poll(); System.out.print(v.toString() + " "); for (Edge<T> edge : adj.get(v)) { T u = edge.neighbor; if (visited.get(u) == null) { q.add(u); visited.put(u, true); } } } System.out.println(); } |
JavaScript
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | //Traversal starting from src, BFS, Time O(V+E), Space O(V) bfsTraversal(src) { if (this.adj.get(src) == null) return; var q = new Array(); var visited = new Map(); q.push(src); visited.set(src, true); while (q.length > 0) { let v = q.shift(); console.log(v.toString() + " "); for (let edge of this.adj.get(v)) { let u = edge.neighbor; if (visited.get(u) == null) { q.push(u); visited.set(u, true); } } } } |
Python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | # Traversal starting from src, BFS, Time O(V+E), Space O(V) def bfsTraversal(self, src): if src not in self.adj: return q = [] visited = {} q.append(src) visited[src] = True while (len(q) > 0): v = q.pop(0) print(str(v) + " ",end = "") for edge in self.adj[v]: u = edge.neighbor if u not in visited: q.append(u) visited[u] = True print() |
Free download
Download weighted graph as adjacency list in Java, JavaScript and Python code
Data structures introduction PDF
What data structure should be used to implement a weighted graph as an adjacency list in Java?
It is HashMap. Traditionally, a weighted graph is implemented as an array of linked lists. However using an array, you have to guess and declare the initial number of nodes in the graph. HashMap doesn’t require that. The code is more clean and flexible when using HashMap.